Quasi-particles and Self-energy within the Multipole Approximation (MPA)

In this tutorial you will learn how to use the Multipole Approximation (MPA) for the frequency description in GW as an alternative to PPA and FF methods.

Prerequisites

• yambo executable (version 5.xx)
• gnuplot, for making plots
• Having completed the following tutorials:

First steps: a walk through from DFT to optical properties

How to obtain the quasi-particle band structure of a bulk material: h-BN

Brief introduction

The multipole approximation is a technique to address the frequency convolution in the GW self-energy analytically...

How to generate inputs

Setting a G0W0 calculation with MPA can be done in a similar way to PPA or FF-RA by using the following command

$ yambo -gw0 m

You will recognize the kind of calculation in the first lines of the generated input:

gw0                              # [R] GW approximation
mpa                              # [R][Xm] Multi Pole Approximation for the Screened Interaction

It can be combined with other command as well. Let's define for instance an input with a specific name for an MPA calculation setting the treatment of the Coulomb potential and verbosity for parallelization:

$ yambo -F mpa_rimV_par.in -gw0 m -r -V par

Let's now generate the following inputs for PPA, MPA and FF-RA calculations:

$ yambo -F ppa.in -gw0 p
$ yambo -F mpa.in -gw0 m
$ yambo -F ffr.in -gw0 r

We can compare the variables corresponding to the different descriptions of the frequency dependence. You may be familiar with PPA from previous tutorials. In this case the polarizability operator, from where W is computed, is numerically evaluated in two frequencies, z = 0, and a pure imaginary frequency PPAPntXp set by default to 1 Ha, from where the parameters of the plasmon pole model are interpolated.

In the full frequency case, the polarizability is evaluated on a grid of frequencies along the real axis. The variable ETStpsXd set by default to 100 define the number of frequency points of the grid, while the variable DmRngeXd corresponds to a damping parameter. As described in the tutorials for optical calculations, it is also possible to specify the energy range along the real frequency axis by setting the variable EnRngeXd, otherwise it is automatically set to the largest energy transition.

At variance with PPA and FF-RA, MPA uses a sampling in the complex frequency plane. You will find similar variables in the MPA input to control the sampling. In this case, ETStpsXm define the number of frequency points, which is equivalent to twice the number of poles used in the MPA model, so it should be set to an even number. EnRngeXm is the energy range along the real frequency axis, while ImRngeXm is the energy range along the imaginary axis, which is set by default to 1 Ha similarly to the PPA case. In case the so called "double parallel sampling" is used, DmRngeXm specifies the imaginary shifts of the sampling branch closer to the real frequency axis: the first shift corresponds to the first point only while the second shift to the rest of the points.

Exercise 1: Run MPA and compare with PPA and FF-RA calculations

Since we are only interested in the different frequency description with PPA, MPA and FF-RA, we can fix the unrelated parameters to the default or to a reasonable value. Let's take for example the PPA input and set

EXXRLvcs=  3187                    RL    # [XX] Exchange    RL components
VXCRLvcs=  3187                    RL    # [XC] XCpotential RL components
% BndsRnXp
   1 | 100 |                             # [Xm] Polarization function bands
%
NGsBlkXp= 3000                    mRy    # [Xm] Response block size
% LongDrXp
 1.000000 | 1.000000 | 1.000000 |        # [Xm] [cc] Electric Field
%
% GbndRnge
   1 | 100 |                             # [GW] G[W] bands range
%
DysSolver= "n"                           # [GW] Dyson Equation solver ("n","s","g")
%QPkrange                                # [GW] QP generalized Kpoint/Band indices
7|7|8|9|

Notice that similarly to other tutorials the range of quasi-particles corresponds to the direct gap of the system, i.e. bands 8 and 9 at the k-point number 7 in the QPkrange variable. We set the same values for the analogous variables in the MPA and FF-RA inputs: BndsRnXm = BndsRnXd = BndsRnXp and LongDrXm = LongDrXd = LongDrXp. Let's now set the variables related to frequency.

In the case of PPA input set

PPAPntXp= 1.00000              Ha    # [Xp] PPA imaginary energy

or leave the default value in eV.

In the FF_RA input set

% DmRngeXd
 0.200000 | 0.200000 |         eV    # [Xd] Damping range
%
ETStpsXd= 400                        # [Xd] Total Energy steps

By varying the number of frequencies in intervals of 50 you can check the convergence of this parameter set to 400.

In the MPA input set

EnSampXm= "2l"                       # [Xm] Frequency sampling in the complex plane ("1l" one line, "2l" two lines)
EnGridXm= "lP"                       # [Xm] Partition along the real axis ("ho" homogeneous, "lP" linear, "qP" quadratic, "cP" cubic)
% EnRngeXm
  0.00000 | 4.00000 |          Ha    # [Xm] Energy range
%
% ImRngeXm
  1.00000 | 1.00000 |          Ha    # [Xm] Imaginary range
%
% DmRngeXm
  0.00000 | 0.10000 |          Ha    # [Xm] Damping range
%
ETStpsXm=  16                        # [Xm] Total Energy steps
IntSolXm= "PT"                       # [Xm] MPA interpolation solver ("LA" linear algebra, "PT" Pade-Thiele)
#mpERdb                              # [Xm] Write to disk MPA poles and residues

Minimal explanation of the MPA input variables:

The value of the EnSampXm variable corresponds to two lines defining a double parallel sampling, the EnGridXm variable defines the type of distribution of points along the real frequency axis, we are using a linear partition in power of 2 as the default value.

The maximum of the real frequency range, EnRngeXm, has been set to 4 Ha, a value slightly below the most energetic transition with 100 bands, which has a value of 123.8 eV (4.55 Ha). You can check that the results are not much sensitive to varying the range from the energy of the larger transition to half its value. The imaginary component ImRngeXm has been set to the same default value of 1 Ha used in the PPA input, while the shifts DmRngeXm have been set to their defaults too, 0 and 0.1 Ha.

The variable ETStpsXm is set to 16 frequency points corresponding to a model with 8 poles, as commented above. You can try to use a different number of poles and check that the selected value is reasonable. Be aware that the parameters controlling the MPA sampling need to be chosen with care according to the specific system and that they can't be converged with standard procedures, for example, a larger number of poles does not always lead to a more accurate result.

The input variable IntSolXm selects between the two possible solvers for the interpolation of the MPA model. Mathematically both are equivalent, although due to the non-linear nature of the system of equations, numerical instabilities may arise specially for a large number of poles, then the Pade-Thiele solver is more stable, but the one based on linear algebra is more flexible and it is use only in rare cases. In practice, for MPA it is recommended to compile Yambo in double precision and avoid using more than 20 poles. Rather than increasing the number of poles, it is recommended to try improving the other parameters of the sampling. Last, it is possible to store an additional database with the interpolated poles and residues of the MPA model by adding the mpERdb label, which is left inactivated for now.

Let's now run the calculations and compare the results

$ yambo -F ppa.in -J pp1_i1Ha_x3Ry_b100
$ yambo -F ffr.in -J ff400_d0.2eV_x3Ry_b100
$ yambo -F mpa.in -J mp8_r0-4i1-1d0-0.1Ha_x3Ry_b100

o-pp1_i1Ha_x3Ry_b100.qp:

K-point            Band               Eo [eV]            E-Eo [eV]          Sc|Eo [eV]

7                  8                -0.411876          -0.332210           2.632103
7                  9                 3.877976           1.047207          -3.890988

o-ff400_d0.2eV_x3Ry_b100.qp:

K-point            Band               Eo [eV]            E-Eo [eV]          Sc|Eo [eV]

7                  8                -0.411876          -0.347396           2.599905
7                  9                 3.877976           1.037291          -3.873562

o-mp8_r0-4i1-1d0-0.1Ha_x3Ry_b100.qp:

K-point            Band               Eo [eV]            E-Eo [eV]          Sc|Eo [eV]

7                  8                -0.411876          -0.349764           2.598567
7                  9                 3.877976           1.038180          -3.875556

As can be notice, the results corresponding to MPA with 8 poles are practically on top of the FF-RA results. The difference between the quasi-particle energies computed with MPA and FF-RA is around 2 meV, while in the case of PPA is around 15 meV. This differences are small since the response of this system is well described by a single pole, however, the difference between PPA and full frequency is expected to increase by an order of magnitude with a larger number of bands and polarizability cutoff.

Exercise 2: Run self-energy calculations

So far we have computed quasi-particles with the Newton method, this means that we are evaluating the self-energy in two frequency points used to solve the linearized quasi-particle equation. Now we will plot the whole frequency dependence of the self-energy and the spectral function.

Let's first make a copy of the input files to keep the previous modifications

$ cp ppa.in ppa_SG.in
$ cp mpa.in mpa_SG.in
$ cp ffr.in ffr_SG.in

Then we regenerate the inputs specifying the Dyson solver to be the one corresponding the Green's function

$ yambo -F ppa.in -gw0 p -g g
$ yambo -F mpa.in -gw0 m -g g
$ yambo -F ffr.in -gw0 r -g g

You will now see and set the following variables

DysSolver= "g"                       # [GW] Dyson Equation solver ("n","s","g")
GEnSteps= 200                        # [GW] Green`s Function (GF) energy steps
% GEnRnge
-40.00000 | 40.00000 |         eV    # [GW] GF energy range
%
% GDmRnge
 0.100000 | 0.100000 |         eV    # [GW] G_gw damping range

We can use the same job identifiers to run the calculations

$ yambo -F ppa_SG.in -J pp1_i1Ha_x3Ry_b100
$ yambo -F ffr.in_SG -J ff400_d0.2eV_x3Ry_b100
$ yambo -F mpa.in_SG -J mp8_r0-4i1-1d0-0.1Ha_x3Ry_b100

Let's plot the results

$ gnuplot

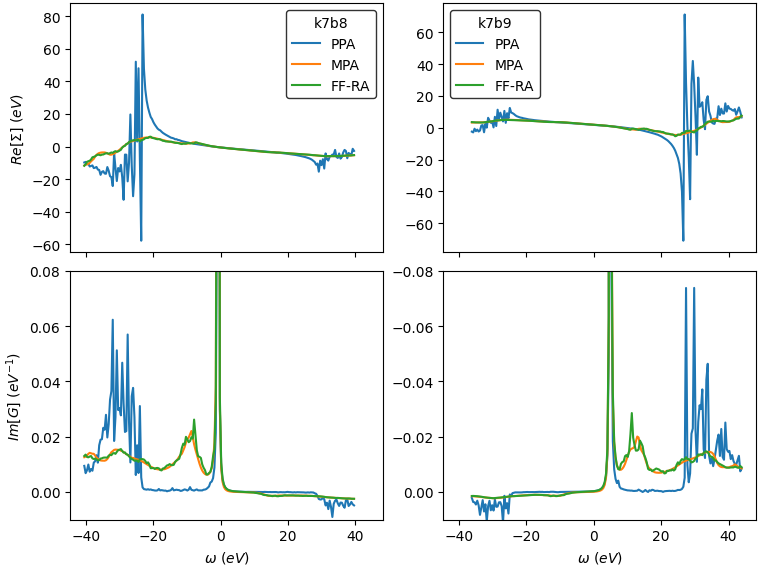
Self-energy:

gnuplot> p "o-pp1_i1Ha_x3Ry_b100.G_Sc_band_008_k_007" u 1:5 w lp, 
           "o-mp8_r0-4i1-1d0-0.1Ha_x3Ry_b100.G_Sc_band_008_k_007" u 1:5 w lp, 
           "o-ff400_d0.2eV_x3Ry_b100.G_Sc_band_008_k_007" u 1:5 w lp

Spectral function:

gnuplot> p "o-pp1_i1Ha_x3Ry_b100.G_Sc_band_008_k_007" u 1:4 w lp, 
           "o-mp8_r0-4i1-1d0-0.1Ha_x3Ry_b100.G_Sc_band_008_k_007" u 1:4 w lp, 
           "o-ff400_d0.2eV_x3Ry_b100.G_Sc_band_008_k_007" u 1:4 w lp

The results for both quasi-particles will be similar to these:

Notice that PPA is only accurate in a zone of the tail of the self-energy corresponding to the quasi-particle peak, while MPA captures all the features in the whole frequency range, including the satellite structures.

Exercise 3: Count unfulfilled modes

We can now examine one of the problems of PPA that concerns the fulfillment of a physical constraint for the poles of W.