Quasi-particles and Self-energy within the Multipole Approximation (MPA)
In this tutorial you will learn how to use the Multipole Approximation (MPA) for the frequency description in GW as an alternative to the plasmon-pole approximation (PPA) and numerical full frequency (FF) methods.
Prerequisites
yamboexecutable (version 5.2)gnuplot, for making plots- Having completed the following tutorials:
First steps: a walk through from DFT to optical properties
How to obtain the quasi-particle band structure of a bulk material: h-BN
Brief introduction
The multipole approximation (MPA) is a technique to address the frequency convolution in the GW self-energy analytically. It can be thought as a generalization of the plasmon-pole approximation (PPA) able to provide full-frequency accuracy at a much lower computational cost than other methods like numerical full frequency integrations on the real axis (FF-RA).
The main concepts to be familiarized with include the design of samplings in the complex frequency plane, the methods to solve the non-linear MPA interpolation, the treatment of unfulfilled modes, and how to run calculations to compute quasi-particle energies and the frequency dependence of the self-energy and the spectral function.
A more detailed description can be found in the papers presenting the MPA method[1], [2].
How to generate inputs
Setting a G0W0 calculation with MPA can be done in a similar way to PPA or FF-RA by using the following command
$ yambo -gw0 m
You will recognize the type of calculation in the first lines of the generated input:
gw0 # [R] GW approximation mpa # [R][Xm] Multi Pole Approximation for the Screened Interaction
It can be combined with other command as well. Let's define for instance an input with a specific name for an MPA calculation setting the treatment of the Coulomb potential and verbosity for parallelization:
$ yambo -F mpa_rimV_par.in -gw0 m -r -V par
Let's now generate the following inputs for PPA, MPA and FF-RA calculations:
$ yambo -F ppa.in -gw0 p $ yambo -F mpa.in -gw0 m $ yambo -F ffr.in -gw0 r
We can compare the variables corresponding to the different descriptions of the frequency dependence. You may be familiar with PPA from previous tutorials. In this case the polarizability operator, from where W is computed, is numerically evaluated in two frequencies, z = 0, and a pure imaginary frequency PPAPntXp set by default to 1 Ha, from where the parameters of the plasmon pole model are interpolated.
In the full frequency case, the polarizability is evaluated on a grid of frequencies along the real axis. The variable ETStpsXd set by default to 100 define the number of frequency points of the grid, while the variable DmRngeXd corresponds to a damping parameter. As described in the tutorials for optical calculations, it is also possible to specify the energy range along the real frequency axis by setting the variable EnRngeXd, otherwise it is automatically set to the largest energy transition.
At variance with PPA and FF-RA, MPA uses a sampling in the complex frequency plane. You will find similar variables in the MPA input to control the sampling. In this case, ETStpsXm define the number of frequency points, which is equivalent to twice the number of poles used in the MPA model, so it should be set to an even number. EnRngeXm is the energy range along the real frequency axis, while ImRngeXm is the energy range along the imaginary axis, which is set by default to 1 Ha similarly to the PPA case. In case the so called "double parallel sampling" is used, DmRngeXm specifies the imaginary shifts of the sampling branch closer to the real frequency axis: the first shift corresponds to the first point only while the second shift to the rest of the points.
Exercise 1: Run MPA and compare with PPA and FF-RA calculations
Since we are only interested in the different frequency description with PPA, MPA and FF-RA, we can fix the unrelated parameters to the default or to a reasonable value. Let's take for example the PPA input and set
EXXRLvcs= 3187 RL # [XX] Exchange RL components
VXCRLvcs= 3187 RL # [XC] XCpotential RL components
% BndsRnXp
1 | 100 | # [Xm] Polarization function bands
%
NGsBlkXp= 3000 mRy # [Xm] Response block size
% LongDrXp
1.000000 | 1.000000 | 1.000000 | # [Xm] [cc] Electric Field
%
% GbndRnge
1 | 100 | # [GW] G[W] bands range
%
DysSolver= "n" # [GW] Dyson Equation solver ("n","s","g")
%QPkrange # [GW] QP generalized Kpoint/Band indices
7|7|8|9|
Notice that similarly to other tutorials on bulk hBN the range of quasi-particles corresponds to the direct gap of the system, i.e. bands 8 and 9 at the k-point number 7 in the QPkrange variable. We set the same values for the analogous variables in the MPA and FF-RA inputs: BndsRnXm = BndsRnXd = BndsRnXp and LongDrXm = LongDrXd = LongDrXp. Let's now set the variables related to frequency.
In the case of PPA input set
PPAPntXp= 1.00000 Ha # [Xp] PPA imaginary energy
or leave the default value in eV.
In the FF_RA input set
% DmRngeXd 0.200000 | 0.200000 | eV # [Xd] Damping range % ETStpsXd= 400 # [Xd] Total Energy steps
By varying the number of frequencies in intervals of 50 you can check the convergence of this parameter set to 400.
In the MPA input set
EnSampXm= "2l" # [Xm] Frequency sampling in the complex plane ("1l" one line, "2l" two lines)
EnGridXm= "lP" # [Xm] Partition along the real axis ("ho" homogeneous, "lP" linear, "qP" quadratic, "cP" cubic)
% EnRngeXm
0.00000 | 4.00000 | Ha # [Xm] Energy range
%
% ImRngeXm
1.00000 | 1.00000 | Ha # [Xm] Imaginary range
%
% DmRngeXm
0.00000 | 0.10000 | Ha # [Xm] Damping range
%
ETStpsXm= 16 # [Xm] Total Energy steps
IntSolXm= "PT" # [Xm] MPA interpolation solver ("LA" linear algebra, "PT" Pade-Thiele)
#mpERdb # [Xm] Write to disk MPA poles and residues
Minimal explanation of the MPA input variables:
The value of the EnSampXm variable corresponds to two lines defining a double parallel sampling, the EnGridXm variable defines the type of distribution of points along the real frequency axis, we are using a linear partition in power of 2 as the default value.
The maximum of the real frequency range, EnRngeXm, has been set to 4 Ha, a value slightly below the most energetic transition with 100 bands, which has a value of 123.8 eV (4.55 Ha). You can check that the results are not much sensitive to varying the range from the energy of the larger transition to half its value. The imaginary component ImRngeXm has been set to the same default value of 1 Ha used in the PPA input, while the shifts DmRngeXm have been set to their defaults too, 0 and 0.1 Ha.
The variable ETStpsXm is set to 16 frequency points corresponding to a model with 8 poles, as commented above. You can try to use a different number of poles and check that the selected value is reasonable. Be aware that the parameters controlling the MPA sampling need to be chosen with care according to the specific system and that they can't be converged with standard procedures, for example, a larger number of poles does not always lead to a more accurate result.
The input variable IntSolXm selects between the two possible solvers for the interpolation of the MPA model. Mathematically both are equivalent, although due to the non-linear nature of the system of equations, numerical instabilities may arise specially for a large number of poles, then the Pade-Thiele solver is more stable, but the one based on linear algebra is more flexible and it is use only in rare cases. In practice, for MPA it is recommended to compile Yambo in double precision and avoid using more than 20 poles. Rather than increasing the number of poles, it is recommended to try tuning better the other parameters of the sampling.
Last, it is possible to store an additional database with the interpolated poles and residues of the MPA model by adding the mpERdb label, which is left inactivated for now.
Let's now run the calculations and compare the results
$ yambo -F ppa.in -J pp1_i1Ha_x3Ry_b100 $ yambo -F ffr.in -J ff400_d0.2eV_x3Ry_b100 $ yambo -F mpa.in -J mp8_r0-4i1-1d0-0.1Ha_x3Ry_b100
o-pp1_i1Ha_x3Ry_b100.qp:
K-point Band Eo [eV] E-Eo [eV] Sc|Eo [eV] 7 8 -0.411876 -0.332210 2.632103 7 9 3.877976 1.047207 -3.890988
o-ff400_d0.2eV_x3Ry_b100.qp:
K-point Band Eo [eV] E-Eo [eV] Sc|Eo [eV] 7 8 -0.411876 -0.347396 2.599905 7 9 3.877976 1.037291 -3.873562
o-mp8_r0-4i1-1d0-0.1Ha_x3Ry_b100.qp:
K-point Band Eo [eV] E-Eo [eV] Sc|Eo [eV] 7 8 -0.411876 -0.349764 2.598567 7 9 3.877976 1.038180 -3.875556
As can be noticed, the results corresponding to MPA with 8 poles are practically on top of the FF-RA results. The difference between the quasi-particle energies computed with MPA and FF-RA is around 2 meV, while in the case of PPA is around 15 meV. This differences are small since the response of this system is well described by a single pole, however, the difference between PPA and full frequency is expected to increase by an order of magnitude with a larger number of bands and polarizability cutoff.
Exercise 2: Run self-energy calculations
So far we have computed quasi-particles with the Newton method, this means that we are evaluating the self-energy in two frequency points used to solve the linearized quasi-particle equation. Now we will plot the whole frequency dependence of the self-energy and the spectral function.
Let's first make a copy of the input files to keep the previous modifications
$ cp ppa.in ppa_SG.in $ cp mpa.in mpa_SG.in $ cp ffr.in ffr_SG.in
Then we regenerate the inputs specifying the Dyson solver to be the one corresponding the Green's function
$ yambo -F ppa.in -gw0 p -g g $ yambo -F mpa.in -gw0 m -g g $ yambo -F ffr.in -gw0 r -g g
You will now see and set the following variables
DysSolver= "g" # [GW] Dyson Equation solver ("n","s","g")
GEnSteps= 200 # [GW] Green`s Function (GF) energy steps
% GEnRnge
-40.00000 | 40.00000 | eV # [GW] GF energy range
%
% GDmRnge
0.100000 | 0.100000 | eV # [GW] G_gw damping range
We can use the same job identifiers to run the calculations
$ yambo -F ppa_SG.in -J pp1_i1Ha_x3Ry_b100 $ yambo -F ffr_SG.in -J ff400_d0.2eV_x3Ry_b100 $ yambo -F mpa_SG.in -J mp8_r0-4i1-1d0-0.1Ha_x3Ry_b100
Let's plot the results
$ gnuplot
Self-energy:
gnuplot> p "o-pp1_i1Ha_x3Ry_b100.G_Sc_band_008_k_007" u 1:5 w lp,
"o-mp8_r0-4i1-1d0-0.1Ha_x3Ry_b100.G_Sc_band_008_k_007" u 1:5 w lp,
"o-ff400_d0.2eV_x3Ry_b100.G_Sc_band_008_k_007" u 1:5 w lp
Spectral function:
gnuplot> p "o-pp1_i1Ha_x3Ry_b100.G_Sc_band_008_k_007" u 1:4 w lp,
"o-mp8_r0-4i1-1d0-0.1Ha_x3Ry_b100.G_Sc_band_008_k_007" u 1:4 w lp,
"o-ff400_d0.2eV_x3Ry_b100.G_Sc_band_008_k_007" u 1:4 w lp
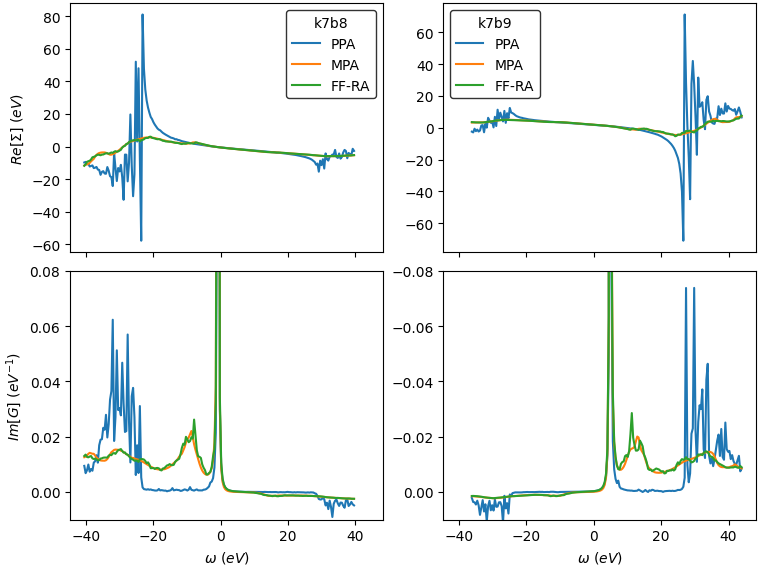
The results for both quasi-particles will be similar to these:
Notice that PPA is only accurate in a zone of the tail of the self-energy corresponding to the quasi-particle peak, while MPA captures all the features in the whole frequency range, including the satellite structures.
Exercise 3: Count unfulfilled modes
We can now examine one of the problems of PPA that concerns the fulfillment of a physical constraint for the poles of W. As an example, for the diagonal elements, W evaluated on the imaginary axis should be real and therefore unfulfilled modes are those for which the interpolated PPA pole is instead imaginary. Since the current implementation of Yambo it is possible to check in the report file some information about unfulfilled modes for each q point.
Let's open the file r-pp1_i1Ha_x3Ry_b100_HF_and_locXC_gw0_em1d_ppa and check the following lines corresponding to the first q point:
Current Q-pt index : 1 :: PP condition fails/total : 0.216216 :: Time ordering fails/rest : 0.500466 :: Mean rel dev of PP cond : 0.216203 Current Q-pt index : 2 ...
In the Exercise 1 we have set the cutoff energy for the size of the polarizability matrix to 3000 mRy, which corresponds to matrices of dimension 37. In the report we can see that the 22% of these matrix elements are identified as unfulfilled modes. In the PPA case the energy of the failing poles is set to a fixed value of 1 Ha, which produces a mean relative standard deviation of 0.22. There is a third variable accounting for the percentage of fulfilled modes with a wrong time ordering. This variable is usually around 50%, since PPA drops the imaginary part of the poles and does't really account for their time ordering.
The condition controlling the fulfillment of the constraint has been generalized to a multipole expression for the MPA case, which also forces all the poles to be compliant with the time ordering. In order to count the unfulfilled modes we need to run the MPA calculation switching on the mpERdb label in the input file. Let's also change the number of poles in the mpa.in file:
ETStpsXm= 4 # [Xm] Total Energy steps mpERdb # [Xm] Write to disk MPA poles and residues
and then
$ yambo -F mpa.in -J mp2_r0-4i1-1d0-0.1Ha_x3Ry_b100
Now we can check the report file r-mp2_r0-4i1-1d0-0.1Ha_x3Ry_b100_HF_and_locXC_gw0_em1d_ppa
:: Current Q-pt index : 1 :: Number of poles : 2 :: PP cond fix/tot : 0.081406 :: Mean np reduction : 0.000000 :: Mean Xm rel dev : 0.079866 ...
You can see that already with 2 poles the number of unfulfilled modes is reduced to 8% and the mean relative deviation to 0.08. In the cases with more than one pole the generalized condition may result in the reduction of the number of poles for a specific matrix element, there is an additional variable in the report accounting for the mean pole reduction in the given matrix.
Since MPA uses an improved condition to fix the nonphysical poles, we can also compare the case of MPA with a single pole with PPA. In order to do so we need to modify the sampling to make it consistent to the one used in PPA. Let's make a copy of the input:
$ cp mpa.in mpa1.in
and set the sampling in mpa1.in as follows:
% EnRngeXm 0.00000 | 0.00000 | Ha # [Xm] Energy range % % ImRngeXm 0.00000 | 1.00000 | Ha # [Xm] Imaginary range % ETStpsXm= 2 # [Xm] Total Energy steps
Then run the calculation and check the output results
$ yambo -F mpa1.in -J mp1_r0-0i0-1Ha_x3Ry_b100
You will find that in cases like this, where the treatment of the unfulfilled modes is important, MPA with a single pole already improves the PPA results:
K-point Band Eo [eV] E-Eo [eV] Sc|Eo [eV] 7 8 -0.411876 -0.346001 2.615150 7 9 3.877976 1.056318 -3.880004
References
- ↑ D. A. Leon, C. Cardoso, T. Chiarotti, D. Varsano, E. Molinari, and A. Ferretti, Frequency dependence in GW made simple using a multipole approximation Phys. Rev. B 104, 115157 (2021)
- ↑ D. A. Leon, A. Ferretti, D. Varsano, E. Molinari, and C. Cardoso, Efficient full frequency GW for metals using a multipole approach for the dielectric screening Phys. Rev. B 107, 155130 (2023)