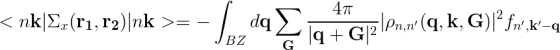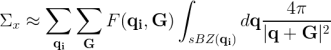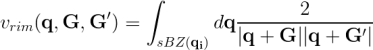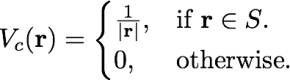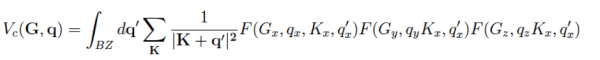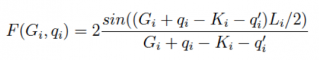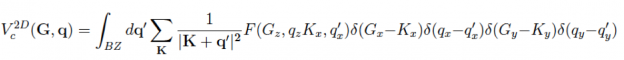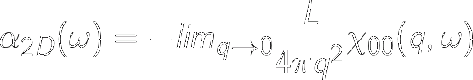How to treat low dimensional systems
In this tutorial you will learn how to treat low-dimensional material. A small k-sampling is used to reduce the computational cost/time. Later on you can repeat this tutorial but using denser k-grids to check the convergence.
Prerequisites
yamboexecutableyppexecutablegnuplot, for plotting spectra- Have Completed the First steps: a walk through from DFT to optical properties tutorial
Avoid numerical divergences using the Random Integration Method (RIM)
In DFT runs of low-dimensional materials low dimensional k-grids are generally used. (i.e. NxNx1 for a 2D sheet perpendicular to the z direction) This can create numerical problems in the convergence of the many-body (MB) results due to the divergence at small q of the coulomb potential, which appears in all the main equations. To eliminate this problem YAMBO uses the so-called Random Integration Method which means to use a Monte Carlo Integration with Random Q-points whose number RandQpts will be given in input. For example the exchange self-energy matrix element which is:
assuming that the integrand is a smooth function of momenta the integral can be approximated as
where the small Brillouin Zones (sBZ) relative to a given q-point are the Brillouin Zones of the momenta vectors lattice. They are chosen in such a way to cover the whole BZ. In the RIM run-level yambo calculates the integrals of the symmetrized Coulomb potential
So we are ready to start the tutorial
First go in the proper directory and have a look if all the required databases are there
$ cd YAMBO_TUTORIALS/hBN-2D/YAMBO $ ls ./SAVE ns.db1 ns.wf ns.kb_pp_pwscf ... $ yambo (initialization, if you haven't already done so)
Create the input to generate the ndb.RIM database
$ yambo -F yambo_WR.in -r
and change the following variables
RandQpts = 1000000 # [RIM] Number of random q-points in the BZ RandGvec = 100 RL # [RIM] Coulomb interaction RS components
N.B RandGvec=100 means to use the RIM for the first 100 G-components of the coulomb potential (Suggestion : later you can check convergence of the HF gap changing these two values) Close input and Run yambo
$ yambo -F yambo_WR.in -J 2D_WR
At the end you find a new database ndb.RIM and a new report file r-2D_WR_rim_cut . Open it and look inside
Gamma point sphere radius [au]: 0.08028
Points outside the sphere : 799246
[Int_sBZ(q=0) 1/q^2]*(Vol_sBZ)^(-1/3) = 7.665674
should be < 7.795600
[WR./2D_WR//ndb.RIM]--------------------------------------
Brillouin Zone Q/K grids (IBZ/BZ): 7 36 7 36
Coulombian RL components : 111
Coulombian diagonal components :yes
RIM random points : 1000000
RIM RL volume [a.u.]: 0.390293
Real RL volume [a.u.]: 0.390112
Eps^-1 reference component :0
Eps^-1 components : 0.00 0.00 0.00
RIM anysotropy factor : 0.000000
- S/N 005962 -------------------------- v.04.01.02 r.00120 -
Summary of Coulomb integrals for non-metallic bands |Q|[au] RIM/Bare:
Q [1]:0.1000E-40.9833 * Q [2]: 0.256404 1.094818 Q [5]: 0.444104 1.032268 * Q [3]: 0.512807 1.024055 Q [6]: 0.678380 1.013997 * Q [4]: 0.769211 1.010774 Q [7]: 0.888208 1.008393
The RIM and Real RL Volumes are quite similar so one million random q-points seems a reasonable number, but again you are invited, later on, to check the convergence of one of the main observables (i.e. HF gap, GW gap, absorption..) changing this number.
Close the report file and perform a calculation of the exchange self-energy to estimate the HF gap (very fast calculation) using the RIM. Generate the input
$ yambo -F yambo_HF_WR.in -J 2D_WR -r -x
In order to calculate the HF gap only for the last k-point (which is the high-simmetry point K) change the last line as Note also that 4 (5) is the highest occupied (lowest unoccupied) band.
%QPkrange # [GW] QP generalized Kpoint/Band indices 7| 7| 4| 5| %
Close the input and run yambo
$ yambo -F yambo_HF_WR.in -J 2D_WR
At the end you will find the report file r-2D_WR_HF_and_locXC_rim_cut and the output file o-2D_WR.hf. Open them and have a look In the output file o-2D_WR.hf you will see
- K-point Band Eo Ehf DFT HF
7.00000 4.00000 0.00000 -3.25329 -16.21953 -19.47282
7.00000 5.00000 4.40109 9.67551 -11.10755 -5.83314
The HF gap is 12.92 eV obtained subtracting the 2 values in the fourth column Now you can do a similar HF calculation without generating and reading the RIM database
$ yambo -F yambo_HF_NR.in -x
change the variables QPkrange as before, close the input and run yambo
$ yambo -F yambo_HF_NR.in -J 2D_NR
in this case the HF gap in the file o-2D_NR.hf results to be 12.69 eV.
Indeed the presence of the numerical instability, discussed before, is evident only using denser k-grids with respect to the one used in this Tutorial (6x6x1) Suggestion: later you can generate other SAVE directories with denser k-grids and check the HF gap. The results of the HF gap calculated with different k-grids without (noRIM) and with Random Integration Method (RIM) to show up the problem are reported:
noRIM RIM
6x6x1 12.69eV 12.92eV 12x12x1 12.80eV 12.92eV 15x15x1 12.96eV 12.93eV 45x45x1 15.52eV 12.96eV
So the home message is : use always the RIM in MB simulations of low-dimensional materials.
Generate a truncated coulomb potential
To simulate an isolated nano-material a convergence with cell vacuum size is in principle required, like in the DFT runs. The use of a truncated Coulomb potential allows to achieve faster convergence eliminating the interaction between the repeated images along the non-periodic direction (see i.e. C. A. Rozzi et al Phys. Rev. B 73, 205119) In this tutorial we learn how to generate a box-like cutoff for a 2D system with the non-periodic direction along z.
In YAMBO you can use :
- spherical cutoff (for 0D systems)
- cylindrical cutoff (for 1D systems)
- box-like cutoff (for 0D, 1D and 2D systems)
The Coulomb potential with a box-like cutoff is defined as
where S is a box-shaped region of the space having sides Lx,Ly and Lz, where they can also assume infinite values (untruncated interaction along desired directions).
Then the FT component is
where
For a 2D-system with non period direction along z-axis we have
Important remarks:
- the Random Integration Method (RIM) is required to perform the Q-space integration
- for sufficiently large supercells a choose L_i slightly smaller than the cell size in the i-direction ensures to avoid interaction between replicas
Create the input file:
$ yambo -F yambo_WR_WC.in -r
Change the RIM Variables as before and activate the cutoff generation
RandQpts = 1000000 # [RIM] Number of random q-points in the BZ RandGvec = 100 RL # [RIM] Coulomb interaction RS components CUTGeo = "box z" # [CUT] Coulomb Cutoff geometry: box/cylinder/sphere X/Y/Z/XY.. % CUTBox 0.00 | 0.00 | 32.0 | # [CUT] [au] Box sides %
Close the input file and run yambo:
$ yambo -F yambo_WR_WC.in -J 2D_WR_WC
in the directory 2D_WR_WC you will find a new database ndb.cutoff
Use the truncated coulomb potential in a G0W0-PPA calculation
Generate the input reading the databases in the 2D_WR_WC directory
$ yambo -J 2D_WR_WC -F yambo_G0W0.in -p p -g n -r -k hartree -V qp In the input change the following variables NGsBlkXp = 4 Ry # [Xp] Response block size QPkrange # [GW] QP generalized Kpoint/Band indices 7| 7| 4| 5|
Close the input and run yambo
$ yambo -F yambo_G0W0.in -J 2D_WR_WC
At the end you will find a new report file r-2D_WR_WC_em1d_ppa_HF_and_locXC_gw0_rim_cut, open it and have a look. You will find also a new output file o-2D_WR_WC.qp. If you open yoi will find that now the G0W0 gap is 4.40 eV (PBE) + 3.70 eV (G0W0 correction) = 8.10 eV Indeed as you have learned in the previous tutorials the correlation part of the self-energy strongly reduces the HF gap. Moreover you should note that the QP correction is larger that one found in the h-BN bulk. Why?
Use the truncated coulomb potential in a BSE calculation
Generate the input for the BSE calculation:
$ yambo -J 2D_WR_WC -F yambo_BSE.in -r -o b -p p -y d -k sex -V all
Some remarks: the largest verbosity is used -V all and a long input file is generated; with the option -p p the static part of the screening matrix is read from the ndb.pp databases
Change the number of G-vectors in the correlation part of the kernel as:
BSENGBlk= 4 Ry # [BSK] Screened interaction block size
use the simple rigid scissor to open the correct the KS energies
% KfnQP_E 3.70000000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim
Set the number of bands to:
% BSEBands 2 | 6 | # [BSK] Bands range
This choice means to include in the BSE only three occupied and 2 unoccupied bands. Increase the number of energy steps
BEnSteps= 500 # [BSS] Energy steps
To do the next Tutorial we need to write the excitonic WFs, so uncomment the following line
#WRbsWF # [BSS] Write to disk excitonic the WFs
Close the input file and run yambo
$ yambo -J 2D_WR_WC -F yambo_BSE.in
Look at the report file r-2D_WR_WC_optics_bse_bsk_bss_em1d_ppa_rim_cut and plot the real and Imaginary part of the dielectric function using the file o-2D_WR_WC.eps_q1_diago_bse.
You realize immediately that the real part of the macroscopic dielectric function is almost 1, while the imaginary part is almost zero. Indeed when the use of the cutoff in the coulomb potential is activated you are simulating a real isolated sheet in vacuum and so you are obtaining almost the dielectric function of vacuum!
For this reason yambo produces another file which contains the macroscopic polarizability (called here 'o-2D_WR_WC.alpha_q1_diago_bse') which is a well defined quantity strictly related to optical conductivity or absorbance.
For a 2D system has the dimension of a length and it is defined as :
where L is the size of the cell in the non-periodic direction (z in this case)
Analyze the differences with corresponding GW and BSE calculations without the use of a truncated coulomb potential
Open the input file yambo_G0W0.in and set back CUTGeo= "none"
Close the input and run yambo
$ yambo -J 2D_WR -F yambo_G0W0.in
You will find a new report r-2D_WR_em1d_ppa_HF_and_locXC_gw0_rim_cut. You are invited to see the difference with the previous one r-2D_WR_WC_em1d_ppa_HF_and_locXC_gw0_rim_cut
and also a new output file o-2D_WR.qp is present. Open and check the QP correction at the last k-point. This time a value of 2.83 eV instead of 3.70 eV is obtained. Are you able to explain this result?
Now redoo the BSE calculation but without reading the cutoff database and applying the QP correction just obtained without using the cutoff.
To do that, open the yambo_BSE.in and put CUTGeo= "none"
and set the QP correction of 2.83 eV, just obtained without uisng the cutoff.
% KfnQP_E 2.830000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim
Close the input file and run yambo
$ yambo -J 2D_WR -F yambo_BSE.in
Plot the imaginary part of the GW and BSE polarizabilities with and withou cutoff:
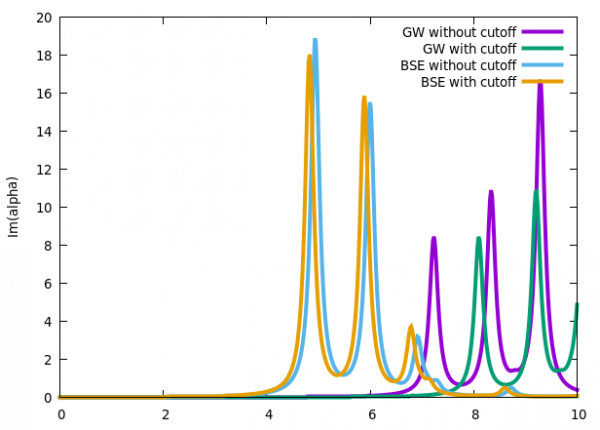
$ gnuplot $ gnuplot> set ylabel 'alpha' $ gnuplot> plot 'o-2D_WR.eps_q1_diago_bse' u 1:($4*33.012/4/pi) w l title 'GW without cutoff' ,'o-2D_WR_WC.alpha_q1_diago_bse' u 1:4 w l title ' GW with cutoff' , 'o-2D_WR.eps_q1_diago_bse' u 1:($2*33.012/4/pi) w l title 'BSE without cutoff' ,'o-2D_WR_WC.alpha_q1_diago_bse' u 1:2 w l title 'BSE with cutoff'
You can note that the energy of the peaks in the two GW spectra (with and without cutoff) are quite different:
you find the first peak around 7 eV without cutoff and around 8 eV with cutoff.
Instead the two GW+BSE spectra, without and with cutoff, are much more similar. Are you able to explain why?
Also note that, for the case without cutoff, to plot the imaginary part of the polarizability, the Imaginary part of the macroscopic dieletric function has been multiplied by the appropriate prefactor.
Remarks: The convergence in k-space can be done separately for GW and BSE calculations, because generally more k-points are needed to converge the excitonic with respect to the quasi-particle properties.
N.B. If you will use the same inputs created in this tutorial remember to set up the cutoff variable CUTGeo= "box z" to use again the truncated coulomb potential in the GW and BSE calculations
Literature on two-dimensional h-BN: L. Wirtz et al Phys Rev Lett 96 126104 (2006), F. Rasmussen et al Phys Rev. B 94 155406 (2016),N. Berseneva et al Phys. Rev. B 87 035404 (2013).