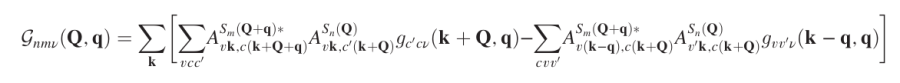Exciton-phonon coupling and luminescence
This an advanced tutorial, we will show how calculate exciton-phonon coupling[1] and phonon-assisted absorption/emission[2].
In order to run this tutorial you need a deep knowledge of the theory involving these processes and on the use of the Yambo code. [3][4][5][6]
We will consider as example bulk hBN. Notice that parameters of the present tutorial are not at convergence, but are enough to get a reasonable result.
The tutorial includes several steps and the calculations can be quite expensive.
In order to calculate luminescence you need electron-phonon matrix elements and excitons (energies and wave-functions) for this reason in this
tutorial we will illustrate the different steps to calculate:
- Electron-phonon matrix elements with Quantum Espresso
- Run the Bethe-Salpter equation for all momementum Q on the same k-grid of the electron-phonon
- Put electron-phonon matrix elements and exciton together to get the final luminescence spectrum
Getting the code
This tutorial works only with Yambo version > 6.x, but a preliminary version of the code is available on github:
https://github.com/attacc/yambo
Notice that this version is not fully tested therefore we advice you do not use it in production. In order to install yambo with exciton-phonon coupling you do:
git clone https://github.com/attacc/yambo.git yambo-excph cd yambo-excph git checkout devel-excph git pull
and the configure Yambo
./configure
and compile the code
make core -j2 make ph-project -j2
notice that -j is for parallel compilation
Electron-phonon matrix elements
Now we need to generate wave-function and the electron-phonon matrix elements that will be used in the exciton-phonon coupling calculations.
This part will take time, but if you want you can skip the databases generation and download them directly here:
If you want to generate the electron-phonon databases and the Kohn-Sham wave-functions, here you will find scripts and all input files to run the a small example on hBN:
In the tgz file you will find a script run_dvscf.sh, a python script and different folders with the QE input files. You have to modify run_dvscf.sh in order to set the correct path of Yambo and QuantumEspresso on your PC, the number of processors to use, and the parallelization command. Then run:
./run_dvscf.sh
it will generate electron-phonon coupling on a Q-grid 12x12x1 for bulk hBN.
Generation of electron-phonon matrix elements can take time,
for example on my PC (core i9) it takes 1 hour with 8 cores. If you want you can decrease the number of K-point up to 8x8 to speed up calculations.
The script will perform self-consistent calculation for the density, then non-self-consistent for the band structure,
calculation of phonons on a special q-grid and finally the calculation of electron-phonon matrix elements.
Notice that the Q-grid is automatically generated from the K point you set for the NSCF calculations.
All these data, wave-functions, and electron-phonon matrix elements are then transformed in the Yambo format.
When the run is finished you can go in the QPT12/dvscf/bn.save folder to start exciton-phonon calculations.
BSE at finite momentum
First of all we need the solution of the Bethe-Salpeter equation for all q-points in the grid.
Run the BSE for all momentum q as explained in the tutorials: BSE basic, BSE convergence, BSE for 2D.
Do not forget to turn on the flag WRbsWF to write the excitonic wave-functions.
You can generate the input for the BSE with the command: yambo_ph -X s -o b -y d -V qp -k sex
em1s # [R][Xs] Statically Screened Interaction optics # [R] Linear Response optical properties bss # [R] BSE solver bse # [R][BSE] Bethe Salpeter Equation. dipoles # [R] Oscillator strenghts (or dipoles) BoseTemp=-1.000000 eV # Bosonic Temperature DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles X_Threads=0 # [OPENMP/X] Number of threads for response functions K_Threads=0 # [OPENMP/BSK] Number of threads for response functions Chimod= "HARTREE" # [X] IP/Hartree/ALDA/LRC/PF/BSfxc BSKmod= "SEX" # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc BSEmod= "resonant" # [BSE] resonant/retarded/coupling BSSmod= "d" # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft` BSENGexx= 14923 RL # [BSK] Exchange components BSENGBlk=-1 RL # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)] #WehCpl # [BSK] eh interaction included also in coupling KfnQPdb= "none" # [EXTQP BSK BSS] Database action KfnQP_INTERP_NN= 1 # [EXTQP BSK BSS] Interpolation neighbours (NN mode) KfnQP_INTERP_shells= 20.00000 # [EXTQP BSK BSS] Interpolation shells (BOLTZ mode) KfnQP_DbGd_INTERP_mode= "NN" # [EXTQP BSK BSS] Interpolation DbGd mode % KfnQP_E 3.000000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim % % BSEQptR 1 | 19 | # [BSK] Transferred momenta range % % BSEBands 7 | 10 | # [BSK] Bands range % % BEnRange 0.00000 | 10.00000 | eV # [BSS] Energy range % % BDmRange 0.100000 | 0.100000 | eV # [BSS] Damping range % BEnSteps= 300 # [BSS] Energy steps % BLongDir 1.000000 | 0.000000 | 0.000000 | # [BSS] [cc] Electric Field % BSEprop= "abs" # [BSS] Can be any among abs/jdos/kerr/magn/dich/photolum/esrt BSEdips= "none" # [BSS] Can be "trace/none" or "xy/xz/yz" to define off-diagonal rotation plane WRbsWF # [BSS] Write to disk excitonic the WFs % BndsRnXs 1 | 16 | # [Xs] Polarization function bands % NGsBlkXs= 51 RL # [Xs] Response block size % LongDrXs 1.000000 | 0.000000 | 0.000000 | # [Xs] [cc] Electric Field %
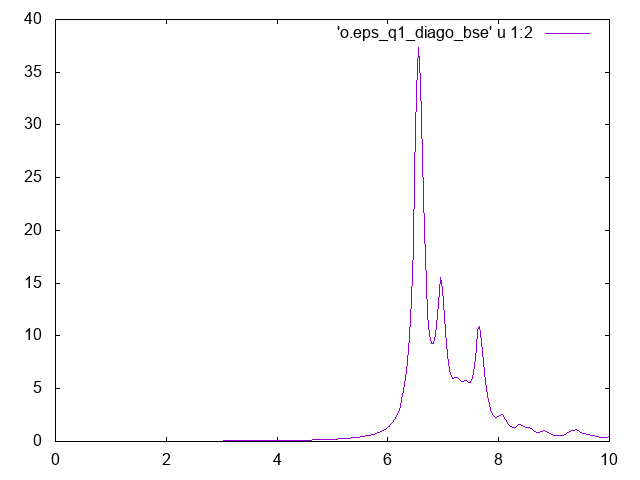
In the BSE we included only the two top valence bands 7,8 and the bottom conduction bands 9,10 plus a scissor of 3.0 eV, and the dielectric constant used to calculate W includes 16 bands and has block size of 51 plane waves. Notice that we calculate the BSE for all the 19 possible transfer momentum. In this input file we used the full diagonalization BSSmod= "d" , for large system it is better to switch to the Slepc libraries, '-y s' in the input file generation. If you plot the optical spectra, file o.eps_q1_diago_bse, you should get something like this:
Exicton dipersion
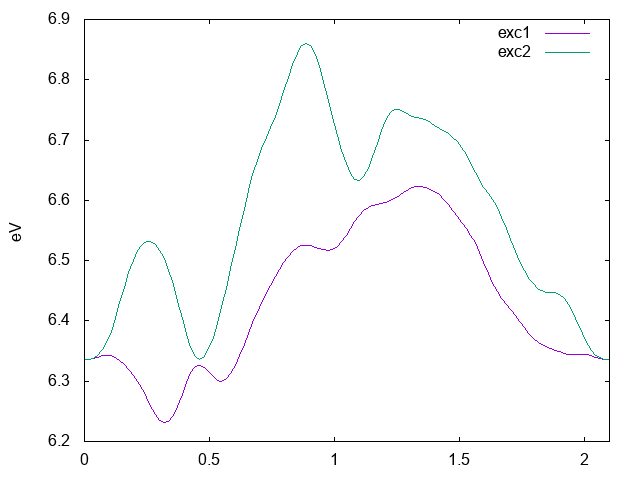
Just to be sure that everything is fine, we can have a look to the exciton dispersion along the path Gamma->K->M->Gamma, with the command: ypp_ph -e i
excitons # [R] Excitonic properties interpolate # [R] Interpolate INTERP_mode= " BOLTZ" # Interpolation mode (NN=nearest point, BOLTZ=boltztrap aproach) INTERP_Shell_Fac= 20.00000 # The bigger it is a higher number of shells is used INTERP_NofNN= 1 # Number of Nearest sites in the NN method BANDS_steps= 50 # Number of divisions cooIn= "rlu" # Points coordinates (in) cc/rlu/iku/alat cooOut= "rlu" # Points coordinates (out) cc/rlu/iku/alat States= "1 - 2" # Index of the BS state(s) % INTERP_Grid -1 |-1 |-1 | # Interpolation BZ Grid % #PrtDOS # Print Exciton Density of States % DOSERange 1.000000 |-1.000000 | eV # Energy range % DOSESteps= 10 # Energy steps DOS_broad= 0.100000 eV # Broadening of the DOS %BANDS_kpts # K points of the bands circuit 0.0 | 0.0 | 0.0 | 0.33333333333| 0.333333333333 | 0.0 | 0.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | %
As you can see in the figure below this system is indirect because the minimum is not a Gamma.
Exciton-phonon matrix elements and optics
Now that you have the BSE for all momentum and the electron-phonon databases, you can create the exciton-phonon matrix elements, according to the equation:
and calculate optical response as:
where Wβα,μq =Eβq − Eα + ωqμ ,for more details see Ref.[7]. Phonon-assisted optical response and exciton-phonon matrix elements can be calculated with the command: yambo_ph -excph o
excph # [R] Exction-phonon ExcGkkp # [R][EXCPH] Exciton-Phonon Matrix Elelements ExcPhOptics # [R][EXCPH] Exciton-Phonon Optics BoseTemp= 0.000000 eV # Bosonic Temperature % ELPhExcStates 1 | 4 | # [EXCPH] Incoming (external) exciton states % % ELPhExcSum 1 | 8 | # [EXCPH] Outgoing (virtual) exciton states % LoutPath= "none" # [EXCPH] Path of the outgoing L FANdEtresh= 10.00000 meV # [ELPH] Energy treshold for Fan denominator LDamping= 0.500000E-3 eV # [EXCPH] Damping of exc-ph self-energy EXCTemp= 20.00000 Kn # [EXCPH] Excitonic Temperature (for luminescence spectra) % ElPhModes 1 | 12 | # [ELPH] Phonon modes included % AlphaQ= 0.000000 # [EXCPH] Excitonic band structure 2D distortion #PLqres # [EXCPH] Write contribution from each q-point #DbGdOnlyPh # [EXCPH] Use Double-Grid only for phonon energies (do not interpolate excitons) #DbGdWEIGHTs # [EXCPH] Use Double-grid also for satellite weights and renormalization #NoMatrxEl # [EXCPH] Set all exciton-phonon matrix elements to one (for testing purpose) % EnRngeXd 5.800000 | 6.400000 | eV # [Xd] Energy range % % DmRngeXd 0.002500 | 0.002500 | eV # [Xd] Damping range % ETStpsXd= 1000 # [Xd] Total Energy steps EXCPHdEtresh= 0.100000E-5 eV # [ELPH] Energy treshold for exc-ph denominator
where the ELPhExcStates state are the one responsible for the absorption and emission, the α indexes in the χαα and ELPhExcSum are the virtual exciton states that enter in the exciton-phonon scattering, namely the β index in the sum χαα. Running the code, Yambo calculates all the exciton-phonon matrix elements and the photon assisted absorption and emission spectra. The emission spectra is calculated using the Roosbroeck–Shockley (RS) relation[8], a Boltzman distribution for the excitonic occupation at temperature EXCTemp, for more detail see Refs.[7][4], other ways for excitonic occupations are possible, for a discussion see Ref.[3].
LoutPath is the path of the outgoing Bethe-Salpeter, in principle one can use two different kind of exciton for virtual and real exciton in above equation. If LoutPath='none' Yambo will read excitons in the same folder of the incoming ones, by default the SAVE folder.
Double grid for exciton and phonon energies is available[2], in order to activate it just generate phonons on large grids and make Yambo reads them, as explained in the electron-phonon tutorial. Yambo automatically will interpolate exciton on the same grid[9]. Using the double-grid, in order to converge results on q-grid you can follow the same strategy of the electron-phonon tutorial: converge the fine grid for fix course grid (matrix elements) and then increase the course one and repeat the process until total convergence is reached.
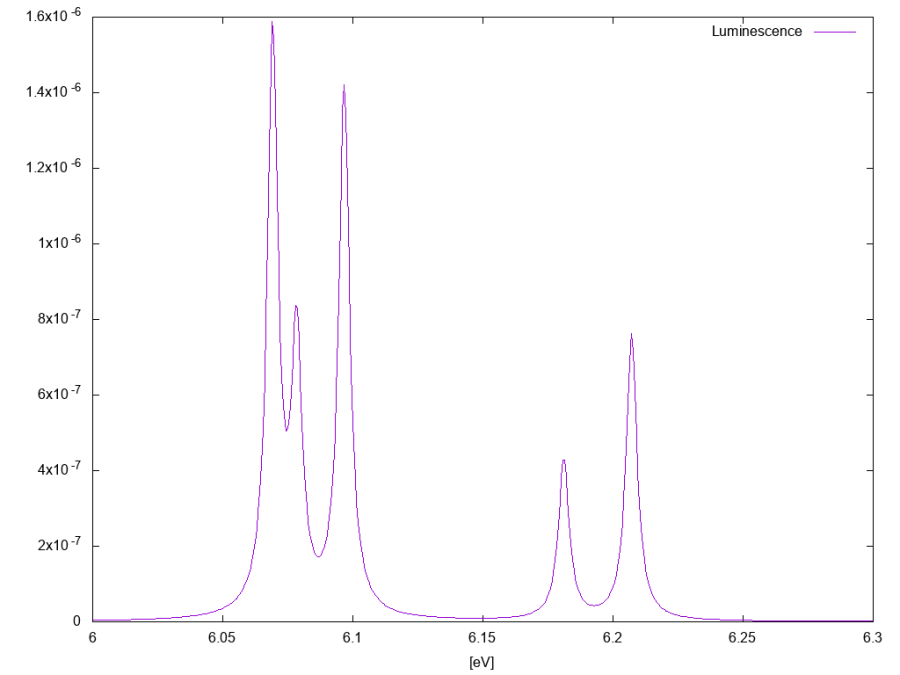
In the output are present two file, the absorption and the luminescence spectra. The absorption is not so interesting because is dominated by a strong direct exciton and phonon-assisted peaks are only slightly visible. Hereafter we plot the luminescence spectrum that can be compared with the ones of Ref.[2][4][5].
WARNING: In the calculation of the exciton-phonon coupling matrix elements, the electron-phonon and BSE coefficients enter with their own phase. This means that to be consistent these matrix elements should be calculated from the same Koth-Sham wave functions. Unfortunately, this is not the case in the current implementation. This fact introduces an error that can affect the intensity of the peaks or also the exciton lifetime, for a better discussion of this problem see Ref.[2],[10] and [11]. We are working on a better version of this code.
References
- ↑ Optical processes in solids, Toyozawa, Yutaka, and Chris Oxlade. Cambridge University Press, (2003).
- ↑ 2.0 2.1 2.2 2.3 First-principles study of luminescence in hexagonal boron nitride single layer: Exciton-phonon coupling and the role of substrate, P Lechifflart, F Paleari, D Sangalli, C Attaccalite PRM 7 (2), 024006 (2023)
- ↑ 3.0 3.1 Theory of phonon-assisted luminescence in solids: Application to hexagonal boron nitride, E. Cannuccia, B. Monserrat and C. Attaccalite, Phys. Rev. B 99, 081109(R) (2019)
- ↑ 4.0 4.1 4.2 Exciton-Phonon Coupling in the Ultraviolet Absorption and Emission Spectra of Bulk Hexagonal Boron Nitride, F. Paleari et al. PRL 122, 187401(2019)
- ↑ 5.0 5.1 Exciton-Phonon Interaction and Relaxation Times from First Principles, Hsiao-Yi Chen, Davide Sangalli, and Marco Bernardi, Phys. Rev. Lett. 125, 107401(2020)
- ↑ Exciton-phonon coupling and phonon-assisted luminescence in hexagonal Boron Nitride nanostructures, PhD Thesis, Pierre Lechifflart (2023)
- ↑ 7.0 7.1 First-principles approaches to the description of indirect absorption and luminescence spectroscopy: exciton-phonon coupling in hexagonal boron nitride, F. Paleari PhD thesis
- ↑ Photon-Radiative Recombination of Electrons and Holes in Germanium, W. van Roosbroeck and W. Shockley, Phys. Rev. 94, 1558 (1954)
- ↑ Warren E. Pickett, Henry Krakauer, and Philip B. Allen, Phys. Rev. B 38, 2721(1988)
- ↑ Distinguishing different stackings in layered materials via luminescence spectroscopy, M. Zanfrognini et al. Phys. Rev. Lett. 131, 206902 (2023)
- ↑ Optical absorption and photoluminescence of single layer boron nitride from a first principles cumulant approach, G. Marini, M. Calandra, P. Cudazzo (https://arxiv.org/abs/2402.03826)