Second-harmonic generation of 2D-hBN

Step 0: Theoretical framework

In this tutorial, we compute the Second-harmonic generation (SHG) from the dynamics of the Bloch-states. The equation-of-motion of the Bloch-states is explained in the tutorial on Linear response from Bloch-states dynamics. Independently of the 'experiment' we simulate, the part of the integration of motion stays the same. This means that any experiment, including non-linear optics, can be performed at the level of the theory listed for the computation of the dielectric function:

• independent (quasi)particle
• time-dependent Hartree (RPA level)
• time-dependent DFT (and DPFT)
• time-dependent Hartree+Screened exchange (BSE level)

What changes when we want to calculate the SHG (or higher harmonics) is:

• the time-dependence of the input electric field and
• the post-processing of the signal

Time dependence of the electric Field: we choose a sinusoidal electric field, thus a monochromatic laser field. This allows one to expand the polarization in the form [math]\displaystyle{ \bf{P}(t) = \sum_{n=-\infty}^{+\infty} \bf{p}_n e^{-i\omega_n t} }[/math] where the coefficient [math]\displaystyle{ \bf{p}_1,...,\bf{p}_n }[/math] are related to [math]\displaystyle{ \chi^{(1)},...,\chi^{(n)} }[/math] through a coefficient depending on a power of the strength of the field (with the power depending on the order of the response).

At difference with a delta-like perturbation, a real-time simulation gives the response at the laser-field only. Then, to obtain the spectrum for the desired range of frequency, we have to perform so many simulations as the frequencies in the desired range.

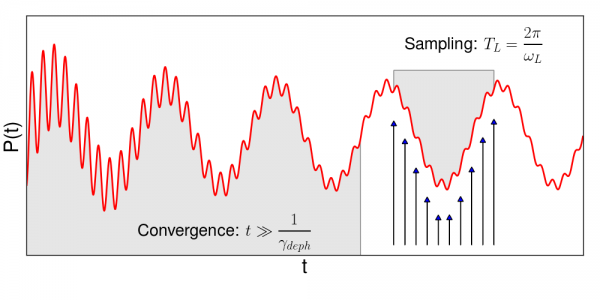
Post-processing of the signal: The switch-on of the electric field corresponds to a weak delta-like kick. Thus, even if it may not be noticeable, the polarization results from both the sinusoidal field and the delta-like kick. The latter excites all eigenfrequencies of the system. Though weak, the resulting signal is comparable with the second-harmonic signal. To eliminate the signal from the eigenfrequencies, we apply a dephasing ([math]\displaystyle{ \gamma_{deph} }[/math]). To have a signal useful to sample the second-harmonic signal, we need to wait a time [math]\displaystyle{ \bar t }[/math] much larger than the dephasing-time [math]\displaystyle{ 1/\gamma_{deph} }[/math]. Note that we cannot choose a too short dephasing time (to shorten the simulation time), as this would result in a too large broadening of the spectrum. After [math]\displaystyle{ \bar t }[/math], we sample $2N+1$ times in a period and use discrete Fourier transform to extract [math]\displaystyle{ {p}_n }[/math] for [math]\displaystyle{ n = 0,...,N }[/math], where n=2 gives the SHG. This is schematically illustrated in figure:

The scheme from Ref. summarised the workflow for computing the SHG (or higher-harmonics) in a energy range [math]\displaystyle{ [\Omega_1,\Omega_2] }[/math].