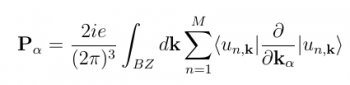Difference between revisions of "Dielectric function from Bloch-states dynamics"
| Line 11: | Line 11: | ||
Where <math> | v_{i \mathbf{k}} \rangle </math> are the time-dependent Bloch states (corresponding to the filled Bloch-states at zero-field), <math>\mathcal E(t)</math> is the external field and the term <math> i e \partial k</math> is the dipole operator consistent with periodic boundary condition. For more details on this last term, see Ref. <ref>I. Souza, J. Íñiguez, and D. Vanderbilt, [https://cfm.ehu.es/ivo/publications/souza_prb04.pdf PRB 69, 085106 (2004)]</ref> and <ref name="Attaccalite2013">C. Attaccalite and M. Gruning [https://arxiv.org/abs/1309.4012v2 Rev. B, '''88''', 235113 (2013)]</ref>. | Where <math> | v_{i \mathbf{k}} \rangle </math> are the time-dependent Bloch states (corresponding to the filled Bloch-states at zero-field), <math>\mathcal E(t)</math> is the external field and the term <math> i e \partial k</math> is the dipole operator consistent with periodic boundary condition. For more details on this last term, see Ref. <ref>I. Souza, J. Íñiguez, and D. Vanderbilt, [https://cfm.ehu.es/ivo/publications/souza_prb04.pdf PRB 69, 085106 (2004)]</ref> and <ref name="Attaccalite2013">C. Attaccalite and M. Gruning [https://arxiv.org/abs/1309.4012v2 Rev. B, '''88''', 235113 (2013)]</ref>. | ||
<math> | <math>h_{rt}</math> is the Hamiltonian, | ||
[[File:H mb.png|400px|center|Many-Body Hamiltonian]]. | [[File:H mb.png|400px|center|Many-Body Hamiltonian]]. | ||
This contains the zero-field eigenvalues | This contains the equilibrium Hamiltonian, that is the zero-field eigenvalues evaluated through DFT; the quasiparticle corrections, evaluated from GW or estimated from experiment, and the variation of the self-energy. The latter is a functional of the density matrix, which is obtained from the Bloch states. | ||
The Hamiltonian and the initial wave-functions are obtained from DFT. Then in order to obtain linear response, we probe the system with a delta function field, that excites all the frequencies at the same footing, and Fourier transforms. | The Hamiltonian and the initial wave-functions are obtained from DFT. Then in order to obtain linear response, we probe the system with a delta function field, that excites all the frequencies at the same footing, and Fourier transforms. | ||
Revision as of 10:44, 19 May 2023
Step 0: Theoretical background
The dynamics of Bloch-states is found by integrating a set of Time Dependent Effective Schrödinger Equations (TD-ESEs). Effective means that an effective Hamiltonian is considered. We consider the many-body effective Hamiltonians seen in the Linear response from real time simulations. In addition, one can also consider effective Hamiltonians based on density-functional theory. The latter choice gives time-dependent density-functional theory.
At difference with what seen in Linear response from real time simulations, the coupling between electrons and the external field is described by means of the Modern Theory of Polarization:
Where [math]\displaystyle{ | v_{i \mathbf{k}} \rangle }[/math] are the time-dependent Bloch states (corresponding to the filled Bloch-states at zero-field), [math]\displaystyle{ \mathcal E(t) }[/math] is the external field and the term [math]\displaystyle{ i e \partial k }[/math] is the dipole operator consistent with periodic boundary condition. For more details on this last term, see Ref. [1] and [2].
[math]\displaystyle{ h_{rt} }[/math] is the Hamiltonian,
.
This contains the equilibrium Hamiltonian, that is the zero-field eigenvalues evaluated through DFT; the quasiparticle corrections, evaluated from GW or estimated from experiment, and the variation of the self-energy. The latter is a functional of the density matrix, which is obtained from the Bloch states.
The Hamiltonian and the initial wave-functions are obtained from DFT. Then in order to obtain linear response, we probe the system with a delta function field, that excites all the frequencies at the same footing, and Fourier transforms.
The hamiltonian is defined as in the case of the equation of motion for the density matrix. Then the polarization is calculated by means of Berry's phase
Note that the equations of motion of Yambo are in the length gauge. Other codes choose instead to work in the velocity gauge. If you want to know more about the advantages and disadvantages of the two gauges read section 2.7 of Ref. [3].
Advantages and disadvantages with respect to the density-matrix based formalism
Yambo implements two distinct formalisms for studying the real-time response, the one based on density-matrix and the one based on Boch states. These formalisms can be used in depending on what we want to simulate. The dynamics formulation in terms of density matrix or non-equilibrium Green's functions allows a systematic treatment of correlation effects and electron-phonon coupling[4], but the price to pay is that the coupling with the external field is correct only to the linear order. This formalism is important in all those phenomena where electronic relaxation plays a major role. On the other hand, in the TDSE formalism the coupling with the external field in an exact way even beyond the linear regime, and for this reason, it allows the description of phenomena coherent with the strong external fields, like the non-linear response.
- ↑ I. Souza, J. Íñiguez, and D. Vanderbilt, PRB 69, 085106 (2004)
- ↑ C. Attaccalite and M. Gruning Rev. B, 88, 235113 (2013)
- ↑ C. Attaccalite, arXiv 1609.09639 (2017)
- ↑ D. Sangalli, and A. Marini EPL 110, 47004 (2015)