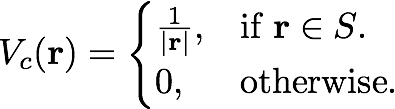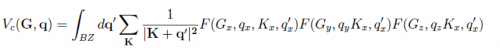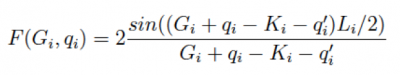Difference between revisions of "How to treat low dimensional systems"
| Line 1: | Line 1: | ||
In this tutorial you will learn how to: | In this tutorial you will learn how to: | ||
* generate a coulomb potential with a box-like cutoff | * generate a truncated coulomb potential with a box-like cutoff | ||
* visualize this coulomb potential | * visualize this truncated coulomb potential | ||
* use this | * use this truncated coulomb in the HF, GW and BSE calculation | ||
* analyze the difference with similar calculations without cutoff | * analyze the difference with similar calculations without using this cutoff | ||
== Prerequisites == | == Prerequisites == | ||
| Line 74: | Line 74: | ||
Close the input and run again yambo | Close the input and run again yambo | ||
At the end you will find some new files | |||
o-2D.RL_components o-2D.xy_plane o-2D.xz_plane o-2D.yz_plane | |||
and you can use gnuplot to plot them | |||
$ gnuplot | |||
gnuplot> plot 'o-2D.RL_components' u 1:2,'o-2D.RL_components' u 1:3 | |||
gnuplot> splot 'o-2D.xy_plane' u 1:2:3,'o-2D.xy_plane' u 1:2:4 | |||
gnuplot> splot 'o-2D.xz_plane' u 1:2:3,'o-2D.xz_plane' u 1:2:4 | |||
Revision as of 14:42, 26 March 2017
In this tutorial you will learn how to:
- generate a truncated coulomb potential with a box-like cutoff
- visualize this truncated coulomb potential
- use this truncated coulomb in the HF, GW and BSE calculation
- analyze the difference with similar calculations without using this cutoff
Prerequisites
- Complete the Generating the Yambo databases tutorial
SAVEfolder for 2D hBN.yamboexecutableyppexecutable- Run Initialization
Generate the cutoff databases (yambo -r)
To simulate an isolated nano-material a convergence with cell vacuum size is in principle required, like in the DFT runs. The use of a truncated Coulomb potential allows to achieve faster convergence eliminating the interaction between the repeated images along the non-periodic direction (see i.e. D. Varsano et al Phys. Rev. B and .. ) In this tutorial we learn how to generate a box-like cutoff for a 2D system with the non-periodic direction along z.
In YAMBO you can use :
spherical cutoff (for 0D systems) cylindrical cutoff (for 1D systems) box-like cutoff (for 0D, 1D and 2D systems)
The Coulomb potential with a box-like cutoff is defined as
Then the FT component is
where
For a 2D-system with non period direction along z-axis we have
Important remarks:
- the Random Integration Method (RIM) is required to perform the Q-space integration
- choose L_i sligthly smaller than the cell size in the i-direction
Create the input
Creation of the input file:
$ yambo -F yambo_cut2D.in -r
Open the input file yambo_cut2D.in
Change the variables inside as:
RandQpts= 1000000 # [RIM] Number of random q-points in the BZ RandGvec= 100 RL # [RIM] Coulomb interaction RS components
CUTGeo= "box z" # [CUT] Coulomb Cutoff geometry: box/cylinder/sphere X/Y/Z/XY.. % CUTBox 0.00 | 0.00 | 32.0 | # [CUT] [au] Box sides
Close the input file
run yambo
$ yambo -F yambo_cut2D.in -J 2D
in the directory 2D you will find the two new databases
ndb.RIM ndb.cutoff
==Visualize the coulomb potential
Generate again the input with an higher level of verbosity $ yambo -r -V RL -F yambo_cut2D.in
Open the input file and uncomment
- CUTCol_test # [CUT] Perform a cutoff test in R-space
Close the input and run again yambo
At the end you will find some new files
o-2D.RL_components o-2D.xy_plane o-2D.xz_plane o-2D.yz_plane
and you can use gnuplot to plot them
$ gnuplot gnuplot> plot 'o-2D.RL_components' u 1:2,'o-2D.RL_components' u 1:3
gnuplot> splot 'o-2D.xy_plane' u 1:2:3,'o-2D.xy_plane' u 1:2:4
gnuplot> splot 'o-2D.xz_plane' u 1:2:3,'o-2D.xz_plane' u 1:2:4