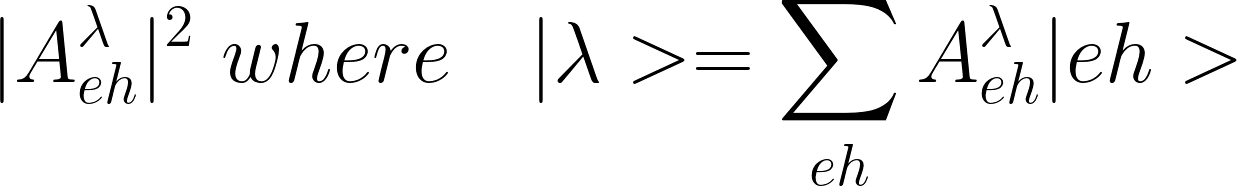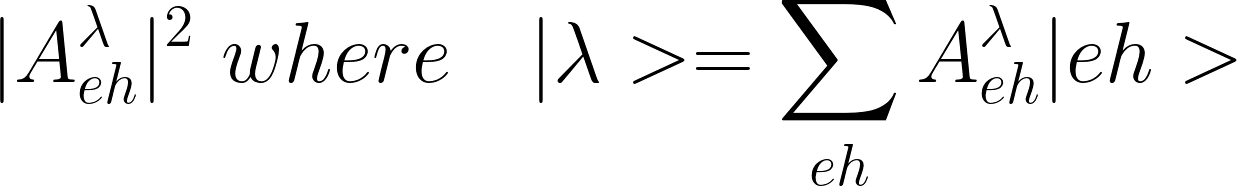Yambo Community Forum

Dear Daniele:
First of all, thank you for your help in the previous topic
Actually, we are very interested in the formulas I mentioned in these two topic, and I am trying to understand the the physics behind these parameters. This is also the reason why I am asking these questions.

Allow me to share my understanding, if you don’t mind.
(1) with we can get the |Aeh|^2 in this equation

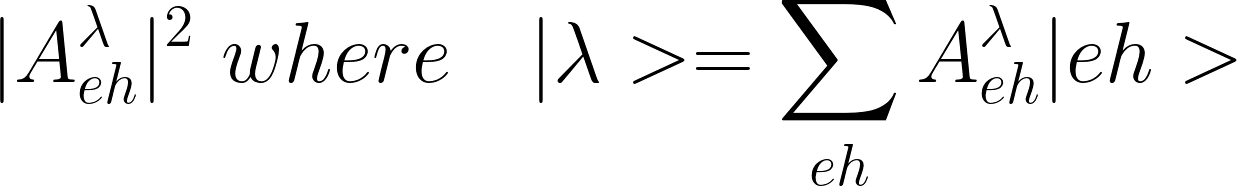
It represents the weights (contributions) at each K-points for a specified excitonic state.
(2) with we get |Aeh*<e|D|h>|^2 in

In which <e|D|h> is optical matrix elements (‘dipoles’), and the value of dipoles determines whether excitons are bright or dark.
(3) Considering this equation, I speculate that Aeh should have a similar form to dipole (but as you mentioned, it should be a scalar). We are curious if it’s possible to use Yambopy to read Aeh over the entire Brillouin zone.
Or, Aeh is a real number, and I only need to take the square root of the amplitude in the o-amplitude?

Thanks again for your help

Dear Jingda,

Yes, you can read the excitonic weights / coefficients A_l^{vck} using yambopy. In particular, if you check this tutorial, you can inspect the sample user script called exc_read.py.

You will see that when the exciton data are loaded with YamboExcitonDB, you then have access to the attribute YamboExcitonDB.eigenvectors. This is a complex-valued numpy array with shapes [N_excitons, N_transitions] and contains all the A-coefficients. Thus, eigenvectors[l,t] means the A-value for exciton l at transition t="vck". The "vck" index is an aggregate transition index: you can see how to extract the individual k, v and c indices from t from the same exc_read.py script.

Have a look also at this post, where some things about the relationship between dipoles, excitonic weights and "residuals" (better called excitonic dipoles) in Yambo is clarified.

Cheers,
Fulvio

Dear Fulvio:
Thank you very much for your reply! This is exactly what I wanted, and I will try it right away.
Furthermore, is my understanding accurate, please?

with ypp -e a -b 1 -F ypp_nodipoles.in
we get |Aeh*<e|D|h>|^2 in

In which <e|D|h> is optical matrix elements (‘dipoles’), and the value of dipoles determines whether excitons are bright or dark.

Update: I found that the dipole file was calculated in step GW, so it should not be related to BSE.
Can I obtain this<e|D|h> by Yambopy?

Dear Jingda,

yes you can read the dipoles and this is explained in the same tutorial indicated by Fulvio:
https://www.yambo-code.eu/wiki/index.ph ... absorption
see YamboDipolesDB

Best,
Daniele

Dear Daniele:
Thank you for your reply.
You may have misunderstood my question. I have already successfully read the dipole data by dipoles_plot.py.
(1) Please forgive my foolishness, but I still want to know if the dipole of excitons is <e | D | h> in


(2) We attempted to use this dipole data, combined with Aeh obtained from YamboExcitonDB, to reproduce the oscillator strength. However, our calculated results clearly did not match the oscillator strength provided by o * exc_qpt_1. We believe this discrepancy arises because the dipole we obtained is the dipole in a single-particle picture (from hole to electron, not exciton). Therefore, can we obtain the dipole of excitons using yambopy?

Dear Jingda,

the exciton dipole is obtained as a linear combination of the singl-particle ones.
Please note:
1) The oscillator strength in o.exc* is normalized to its maximum, normalization factor is reported.
2) The strenght is defined as:
Residuals(:)*real(spin_occ,SP)/(2._SP*pi)**3*d3k_factor*4._SP*pi/q_norm*HA2EV

where:
Residual=\Sum_cv |Acv<c|d|v>|^2
d3k_factor=Vol_bz/Nk
q_norm=q^2, for q=0 is the q0 limit and q0=1e-5
HA2EV=27.2113834_SP

Essentially is the numerator (for a given lambda) of slide 11a in the Yambo cheatsheet:
https://www.yambo-code.eu/wiki/images/c ... et-5.0.pdf

Best,
Daniele

Dear Daniele:
Please let me give an example.
If my ground state exciton is basically formed by one single transition (k,c,v = Γ,11,10), the exciton dipole of this exciton is solely determined by the single-particle(hole and electron) dipole of this transition. This single-particle dipole can be obtained from ydip.dipoles [0, *,10.9]. If the value of the dipoles is very small, the exciton would be dark.
If an exciton formed by two transition, the exciton dipole is the weighted sum of single-particle dipoles of these two transition.
Right?

Dear Jingda,
yes that's correct.

Best,
Daniele

Dear Daniele:
Thank you very much for your patience and explanation！
I have benefited a lot from it