Yambopy tutorial: band structures
This tutorial will show you how to visualise wave-function and band-structure related information, such as atomic, orbital and spin projections, following a DFT Quantum Espresso calculation using the "qepy" module of Yambopy. It also contains a section about Yambo and GW band structures.
The full tutorial, including the Quantum espresso and Yambo databases that we will read, can be downloaded and extracted from the yambo website:
$wget https://media.yambo-code.eu/educational/tutorials/files/databases_qepy.tar.gz $tar -xvzf databases_qepy.tar.gz $cd databases_qepy
Tutorial 1. BN (semiconductor). Band structure
First enter in the folder
cd databases_qepy/bn-semiconductor
and have a look to the
vim plot-qe-bands.py
The qepy classes are useful both to execute Quantum Espresso and to analyze the results. Enter in the python environment, by typing python, then the full qepy library is imported by simply doing:
from qepy import *
Plot Band structure
The qepy class PwXML reads the data file generated by Quantum Espresso and post-processes the data. The class is instanced by doing:
xml = PwXML(prefix='bn', path='bands')
The variable prefix corresponds to the same variable of the QE input. The folder location is indicated by variable path. In order to plot the bands, we also define the k-points path (in crystal coordinates) using the function Path:
npoints = 50
path_kpoints = Path([ [[0.0, 0.0, 0.0],'$\Gamma$'],
[[0.5, 0.0, 0.0],'M'],
[[1./3,1./3,0.0],'K'],
[[0.0, 0.0, 0.0],'$\Gamma$']], [int(npoints*2),int(npoints),int(sqrt(5)*npoints)])
It is worth to note that the path should coincide with the selected path for the QE band calculations.
In order to show the plot we call the plot_eigen method of the PwXML class:
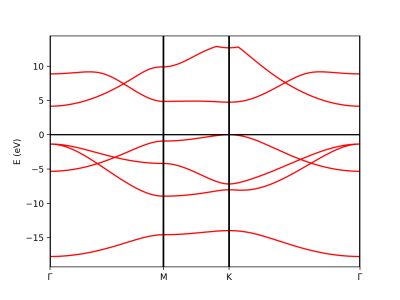
xml.plot_eigen(path_kpoints)
This function will automatically plot the bands as shown below running the script:
python plot-qe-bands.py
Alternatively, we can use the function plot_eigen_ax. This functions requires as input a matplotlib figure object with given axes, as you will see in the next example.
Plot atomic orbital projected Band structure
In addition to the band structure, useful information regarding the atomic orbital nature of the electronic wave functions can be displayed using the class ProjwfcXML. In order to make quantum espresso calculate the relevant data, we need to use the QE executable projwfc.x, which will create the file atomic_proj.xml. This executable projects the Kohn-Sham wavefunctions onto orthogonalized atomic orbitals, among others functionalities. The orbital indexing and ordering are explained in the input documentation of the projwfc.x function which you are invited to check (https://www.quantum-espresso.org/Doc/INPUT_PROJWFC.html#idm94). We can run projwf.x directly from the python script using the qepy class ProjwfcIn:
proj = ProjwfcIn(prefix='bn') proj.run(folder='bands')
Be aware that this can take a while in a large system with many k-points. As in the class PwXML, we then define the path_kpoints and also the selected atomic orbitals to project our bands. We have chosen to represent the projection weight onto the nitrogen (1) and boron (2) orbitals, which according to the projection orderings is given by
atom_1 = list(range(16)) atom_2 = list(range(16,32))
The full list of orbitals is written in the file bands/prowfc.log. We have also defined the figure box
import matplotlib.pyplot as plt fig = plt.figure(figsize=(5,7)) ax = fig.add_axes( [ 0.12, 0.10, 0.70, 0.80 ])
The class ProjwfcXML then runs as in this example:
band = ProjwfcXML(prefix='bn',path='bands',qe_version='7.0') band.plot_eigen(ax,path_kpoints=path_kpoints,cmap='viridis',selected_orbitals=atom_1,selected_orbitals_2=atom_2)
We can run now the file:
python plot-qe-orbitals.py
We have chosen the colormap 'viridis' (variable cmap). You see that the colormap goes from maximum selected_orbitals content (in this case nitrogen) to the maximum selected_orbitals_2 content (in this case boron). The colormap can be represented in many ways and qepy does not include a particular function for this. An example is:
import matplotlib as mpl
cmap=plt.get_cmap('viridis')
bx = fig.add_axes( [ 0.88, 0.10, 0.05, 0.80 ])
norm = mpl.colors.Normalize(vmin=0.,vmax=1.)
cb1 = mpl.colorbar.ColorbarBase(bx, cmap=cmap, norm=norm,orientation='vertical',ticks=[0,1])
cb1.set_ticklabels(['B', 'N'])
We can also plot the band orbital charater with size variation instead of a color scale. In this case we have to pass only the variable selected_orbitals (see the next tutorial).
Tutorial 2. Iron. Ferromagnetic metalic material
In the case of spin-polarized calculations we can plot the spin up and down band structures. We have included in the tutorial a small workflow example to run quantum espresso calculations from scratch. This is done using the classes Tasks and Flows developed in yambopy. You can check the file flow-iron.py for an example. Yambopy includes basic predefined workflows to run the common QE and Yambo calculations. In this case we are using the class PwBandsTasks.
python flow-iron.py
In order to plot the spin-polarized bands. After doing all the calculations from scratch with the flows (flow-iron.py), we can make the band plot by running the script:
python plot-qe-bands.py
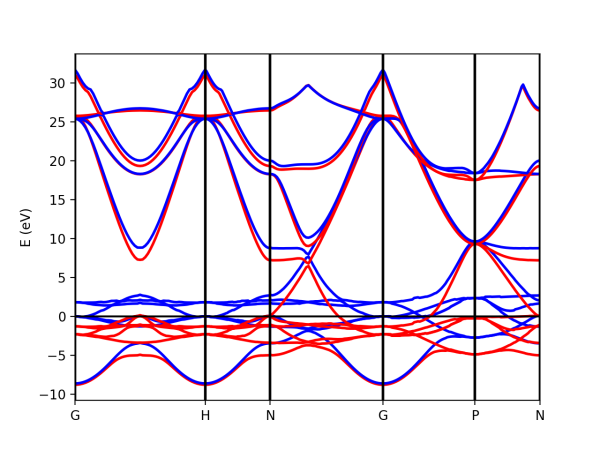
The class PwXML automatically detects the spin polarized case (nspin=2 in the QE input file). The spin up channel is displayed with red and the spin down channel with blue. In the case of iron we have selected this k-point path:
npoints = 50
path_kpoints = Path([ [[0.0, 0.0, 0.0 ],'G'],
[[0.0, 0.0, 1.0 ],'H'],
[[1./2,0.0,1./2.],'N'],
[[0.0, 0.0, 0.0 ],'G'],
[[1./2, 1./2, 1./2 ],'P'],
[[1./2,0.0,1./2. ],'N']], [npoints,npoints,npoints,npoints,npoints])
xml = PwXML(prefix='pw',path='bands/t0') xml.plot_eigen(path_kpoints)
The analysis of the projected atomic orbitals is also implemented. In this case the results are more cumbersome because the projection is separated in spin up and down channels.
Let us look first at the file plot-qe-orbitals-size.
NB: If you generated the quantum espresso databases using the flows instead of relying on the precomputed databases, you also need to rerun the quantum espresso executable projwfc.x to recompute the orbital projections. In this case, please uncomment the following lines in the script (plot-qe-orbitals-size.py) :
#proj = ProjwfcIn(prefix='pw') #proj.run(folder='bands/t0')
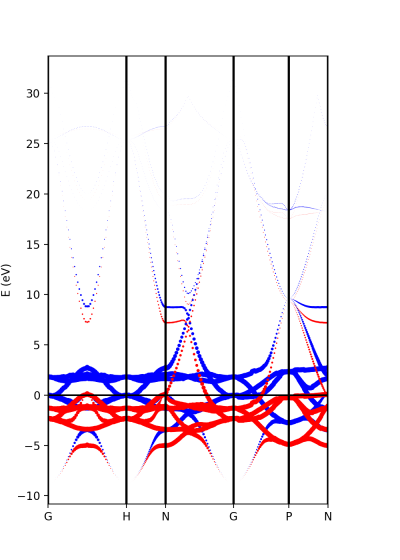
Now, we can use the dot size as a function of the weight of the orbitals
atom_s = [8] atom_p = [0,1,2] atom_d = [3,4,5,6,7]
and the plots are done with
band = ProjwfcXML(prefix='pw',path='bands/t0',qe_version='7.0') band.plot_eigen(ax,path_kpoints=path_kpoints,selected_orbitals=atom_s,color='pink',color_2='black') band.plot_eigen(ax,path_kpoints=path_kpoints,selected_orbitals=atom_p,color='green',color_2='orange') band.plot_eigen(ax,path_kpoints=path_kpoints,selected_orbitals=atom_d,color='red',color_2='blue')
As an example, we can select just the d orbitals by commenting the first two plots and then running the file:
plot-qe-orbitals-size.py
From the plot is clear that d orbitals are mainly localized around the Fermi energy. The plot above is in red and blue, while the default choice in your script should be pink and black. You can experiment with the colors and other matplotlib plot options and also plot the other orbital types.
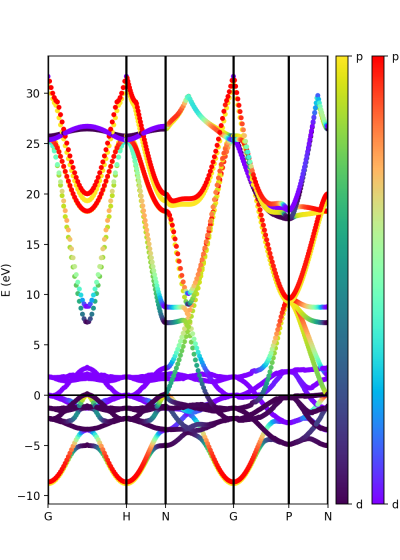
Another option is to plot the orbital composition as a colormap running the file:
plot-qe-orbitals-colormap.py
Here we have added the p and d orbitals in the analysis:
atom_p = [0,1,2] atom_d = [3,4,5,6,7] band = ProjwfcXML(prefix='pw',path='bands/t0',qe_version='7.0') band.plot_eigen(ax,path_kpoints=path_kpoints,cmap='viridis',cmap2='rainbow',selected_orbitals=atom_p,selected_orbitals_2=atom_d)
The colormap bar is added in the same way as in Tutorial 1 (see script), but this time we have a different colormap for each spin polarisation.
Tutorial 3: GW bands
Yambopy can be used either to run Yambo and QE calculations, or to analyse the results of QE and Yambo by dealing with their generated databases. This is done with a variety of classes included in the qepy (for QE) or yambopy (for Yambo) modules. In the case of Yambo GW quasi-particle calculations, we can use the yambopy class YamboQPDB to read the database produced by the simulation. Enter in the folder
cd ../gw-bands
We can use this to find the scissor operator, plot the GW bands and to interpolate the GW bands on a smoother k-path. The example runs by typing:
python plot-qp.py
See below for an explanation of the tutorial. As usual, we can import the qepy and yambopy libraries:
from qepy import * from yambopy import * import matplotlib.pyplot as plt
We define the k-points path.
npoints = 10
path = Path([ [[ 0.0, 0.0, 0.0],'$\Gamma$'],
[[ 0.5, 0.0, 0.0],'M'],
[[1./3.,1./3., 0.0],'K'],
[[ 0.0, 0.0, 0.0],'$\Gamma$']], [int(npoints*2),int(npoints),int(sqrt(5)*npoints)] )
Importantly, the number of points is a free choice. We can increase the variable npoints as we wish, it just means that the interpolation step will take more time. In order to analyse GW results we need to have the file related to the basic data of our Yambo calculation (SAVE/ns.db1) and the netcdf file with the quasi-particle results (ndb.QP). We load the data calling the respective classes:
# Read Lattice information from SAVE lat = YamboSaveDB.from_db_file(folder='SAVE',filename='ns.db1') # Read QP database ydb = YamboQPDB.from_db(filename='ndb.QP',folder='qp-gw')
(in the yambopy module, each class is specialised to read a specific Yambo database)
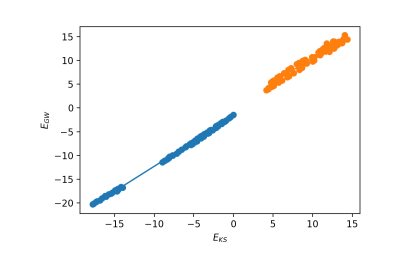
The first option is to plot the energies and calculate the ideal Kohn-Sham to GW scissor operator. We need to select the index of the top valence band:
n_top_vb = 4 ydb.plot_scissor_ax(ax,n_top_vb)
Yambopy displays the fitting and also the data of the slope of each fitting. Notice that this is also a test if the GW calculations are running well. If the dependence is not linear you should double-check your results!
In this case the slope is:
valence bands: slope: 1.0515886598785766 conduction bands: slope: 1.026524081134514 scissor list (shift,c,v) [eV,adim,adim]: [1.8985204833551723, 1.026524081134514, 1.0515886598785766]
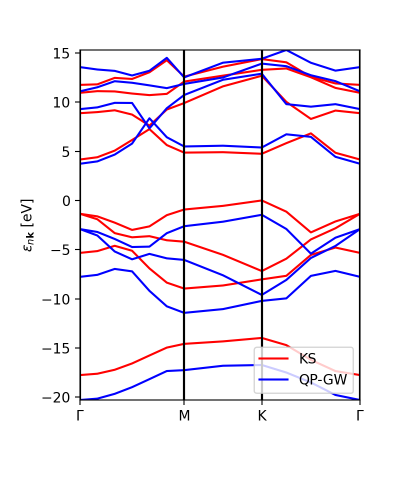
In addition to the scissor operator, we can plot the GW (and DFT) band structure along the path. The first choice would be to plot the actual GW calculations, without interpolation, to check that the results are meaningful (or not). This plot is independent of the number of k-points (npoints) that we want to put in the interpolation. The class YamboQPDB finds the calculated points that belong to the path and plots them. Be aware that if we use coarse grids the class would not find any point and the function will not work.
ks_bs_0, qp_bs_0 = ydb.get_bs_path(lat,path) ks_bs_0.plot_ax(ax,legend=True,c_bands='r',label='KS') qp_bs_0.plot_ax(ax,legend=True,c_bands='b',label='QP-GW')
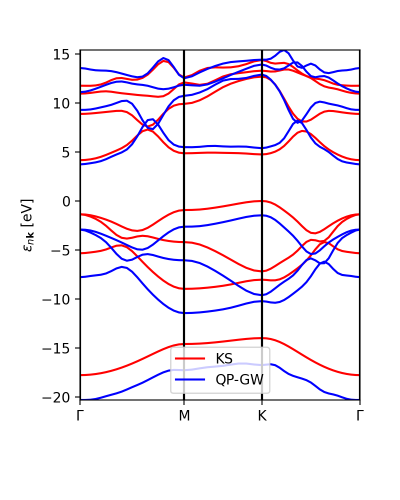
The interpolation of the DFT and GW band structures looks similar:
ks_bs, qp_bs = ydb.interpolate(lat,path,what='QP+KS',lpratio=20) ks_bs.plot_ax(ax,legend=True,c_bands='r',label='KS') qp_bs.plot_ax(ax,legend=True,c_bands='b',label='QP-GW')
The lpratio can be increased if the interpolation does not work as well as intended. The interpolation is the same one implemented in abipy and currently requires abipy installed in order to work.
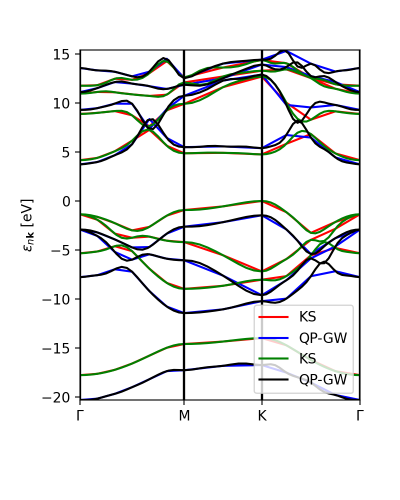
Finally, we can compare the calculated GW eigenvalues with the interpolation.
Links
- Back to Rome 2023#Tutorials
- Back to ICTP 2022#Tutorials